Regularized (Penalized) Linear Regression

class: center, middle, inverse, title-slide

.title[
# Regularized (Penalized) Linear Regression
]
.author[
### Cengiz Zopluoglu
]
.institute[
### College of Education, University of Oregon
]

---

<style>

.blockquote {
  border-left: 5px solid #007935;
  background: #f9f9f9;
  padding: 10px;
  padding-left: 30px;
  margin-left: 16px;
  margin-right: 0;
  border-radius: 0px 4px 4px 0px;
}

#infobox {
  padding: 1em 1em 1em 4em;
  margin-bottom: 10px;
  border: 2px solid black;
  border-radius: 10px;
  background: #E6F6DC 5px center/3em no-repeat;
}

.centering[
  float: center;
]

.left-column2 {
  width: 50%;
  height: 92%;
  float: left;
  padding-top: 1em;
}

.right-column2 {
  width: 50%;
  float: right;
  padding-top: 1em;
}

.remark-code {
  font-size: 18px;
}

.tiny .remark-code { /*Change made here*/
  font-size: 75% !important;
}

.tiny2 .remark-code { /*Change made here*/
  font-size: 50% !important;
}

.indent {
  margin-left: 3em;
}

.single {
  line-height: 1 ;
}

.double {
  line-height: 2 ;
}

.title-slide h1 {
  padding-top: 0px;
  font-size: 40px;
  text-align: center;
  padding-bottom: 18px;
  margin-bottom: 18px;
}

.title-slide h2 {
  font-size: 30px;
  text-align: center;
  padding-top: 0px;
  margin-top: 0px;
}

.title-slide h3 {
  font-size: 30px;
  color: #26272A;
  text-align: center;
  text-shadow: none;
  padding: 10px;
  margin: 10px;
  line-height: 1.2;
}

</style>

### Today's Goals:

- A conceptual introduction to Regularized Regression
  
  - Ridge Regression
  
  - Lasso Regression
  
  - Elastic Net
  
- Implementation with the `glmnet` package

- Building Regularized Regression models with the `caret` package

---

### What is regularization?

- Regularization is a general strategy to incorporate additional penalty terms into the model fitting process

- It is implemented in a various of other algorithms, not just regression.

- The idea behind the regularization is to constrain the size of model coefficients to reduce their sampling variation and, hence, reduce the variance of model predictions.

- The reduction in the variance comes with an expense of bias in model predictions.

- These constraints are typically incorporated into the loss function to be optimized.

- bias - variance tradeoff

- There are two commonly used regularization strategies:

- ridge penalty 
  
  - lasso penalty
  
  - elastic net (a mix of ridge and lasso penalty)

---

# Ridge Regression
---

### Ridge Penalty

- The loss function for the unregularized linear regression: the sum of squared residuals across all observations.

`$$\sum_{i=1}^{N}\epsilon_{(i)}^2$$`

- For ridge regression, we add a penalty term to this loss function, which is a function of all the regression coefficients in the model.

`$$Penalty = \lambda \sum_{i=1}^{P}\beta_p^2,$$`

- `$\lambda$` is a parameter that penalizes the regression coefficients when they get larger.

- Loss function to optimize for the ridge regression:

`$$Loss = \sum_{i=1}^{N}\epsilon_{(i)}^2 + \lambda \sum_{p=1}^{P}\beta_p^2,$$`

---

Let’s consider the same example from the previous class. Suppose that we would like to predict the target readability score for a given text from the Feature 220.

`$$Y = \beta_0  + \beta_1X + \epsilon$$`

Assume the set of coefficients are { `$\beta_0,\beta_1$` } = {-1.5,2}, so my model is
`$$Y = -1.5  + 2X + \epsilon.$$`

Then, the value of the loss function when `$\lambda=0.2$` would be equal to 19.02.

.pull-left[
.single[
.tiny2[

```r
d <- readability_sub[,c('V220','target')]

b0 = -1.5
b1 = 2

d$predicted <- b0 + b1*d$V220
d$error <- d$target - d$predicted

d
```

```
          V220      target  predicted       error
1  -0.13908258 -2.06282395 -1.7781652 -0.28465879
2   0.21764143  0.58258607 -1.0647171  1.64730321
3   0.05812133 -1.65313060 -1.3837573 -0.26937327
4   0.02526429 -0.87390681 -1.4494714  0.57556460
5   0.22430885 -1.74049148 -1.0513823 -0.68910918
6  -0.07795373 -3.63993555 -1.6559075 -1.98402809
7   0.43400714 -0.62284268 -0.6319857  0.00914304
8  -0.24364550 -0.34426981 -1.9872910  1.64302120
9   0.15893717 -1.12298826 -1.1821257  0.05913740
10  0.14496475 -0.99857142 -1.2100705  0.21149908
11  0.34222975 -0.87656742 -0.8155405 -0.06102693
12  0.25219145 -0.03304643 -0.9956171  0.96257066
13  0.03532625 -0.49529863 -1.4293475  0.93404886
14  0.36410633  0.12453660 -0.7717873  0.89632394
15  0.29988593  0.09678258 -0.9002281  0.99701073
16  0.19837037  0.38422270 -1.1032593  1.48748196
17  0.07807041 -0.58143038 -1.3438592  0.76242880
18  0.07935690 -0.34324576 -1.3412862  0.99804044
19  0.57000953 -0.39054205 -0.3599809 -0.03056111
20  0.34523284 -0.67548411 -0.8095343  0.13405021
```
]]]

.pull-right[
.single[
.tiny2[

```r
lambda = 0.2

SSR <- sum((d$error)^2)
penalty <- lambda*(b0^2 + b1^2)
loss <- SSR + penalty

SSR
```

```
[1] 17.76657
```

```r
penalty
```

```
[1] 1.25
```

```r
loss
```

```
[1] 19.01657
```
]]]

---

- Note that when `$\lambda$` is equal to zero, the loss function is identical to SSR; therefore, it becomes a linear regression with no regularization.

- As the value of `$\lambda$` increases, the degree of penalty linearly increases.

- The `$\lambda$` can technically take any positive value between 0 and `$\infty$`.

- A visual representation of the effect of penalty terms on the loss function and regression coefficients

![](ridge.gif)
---

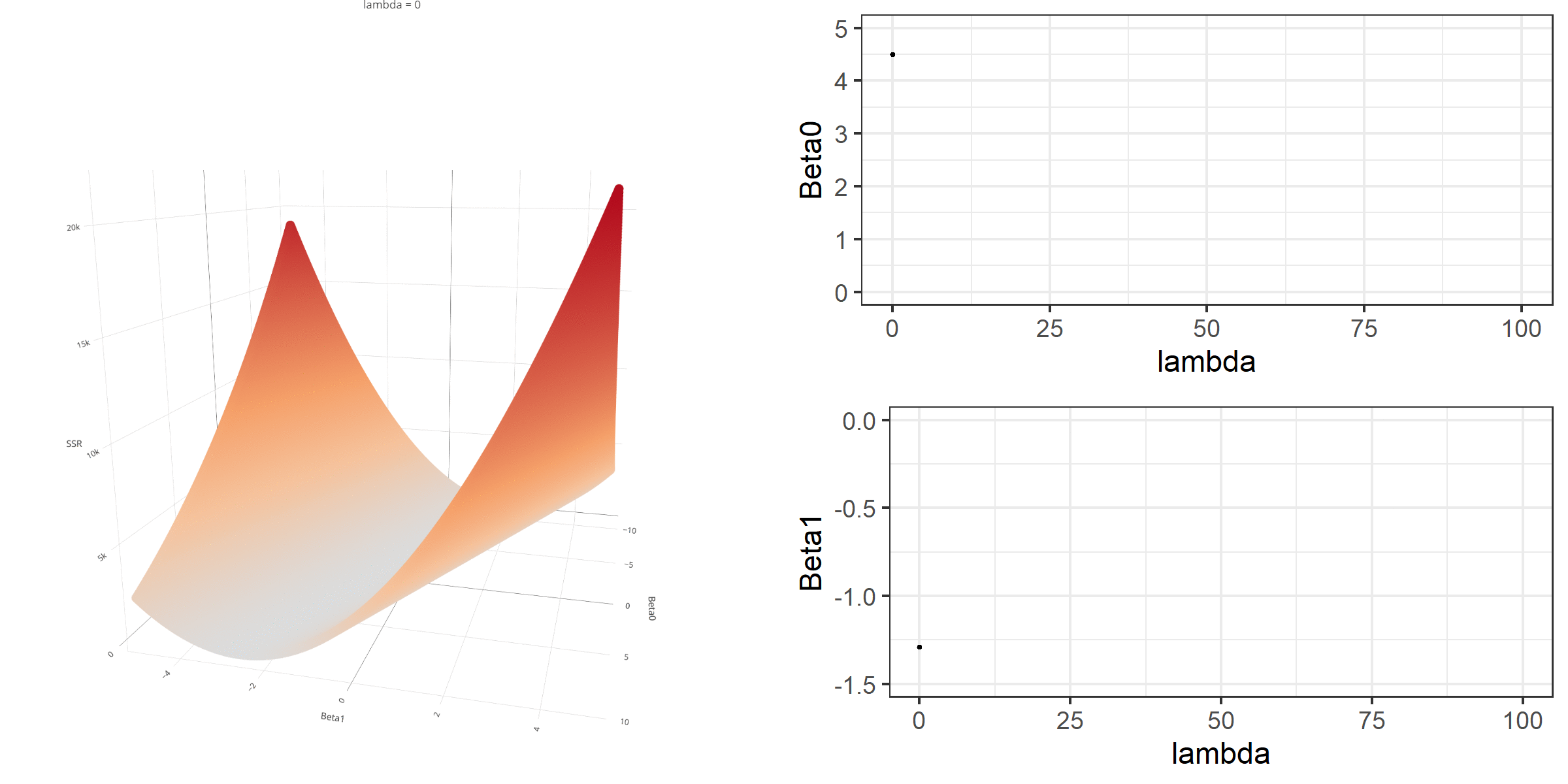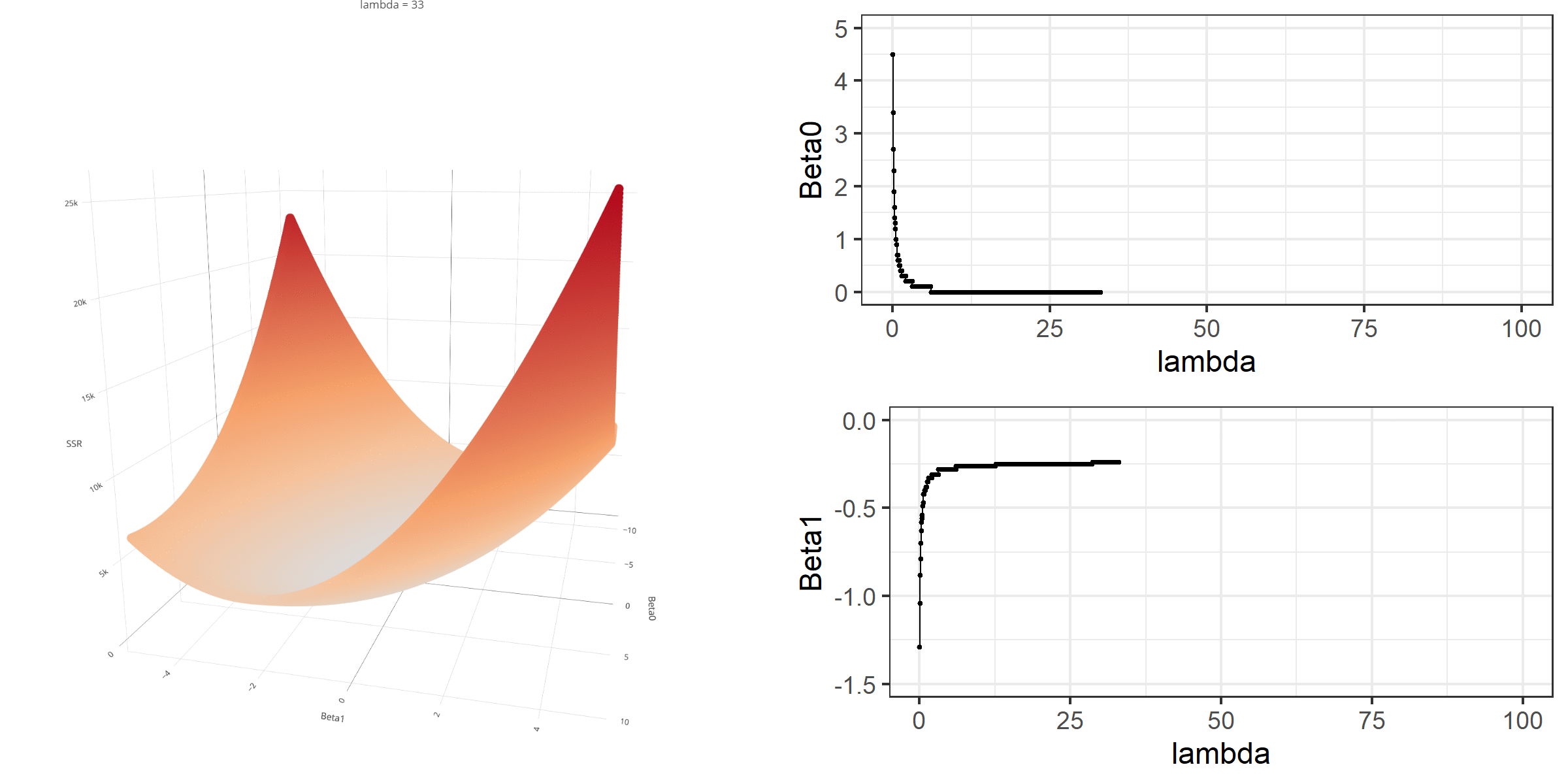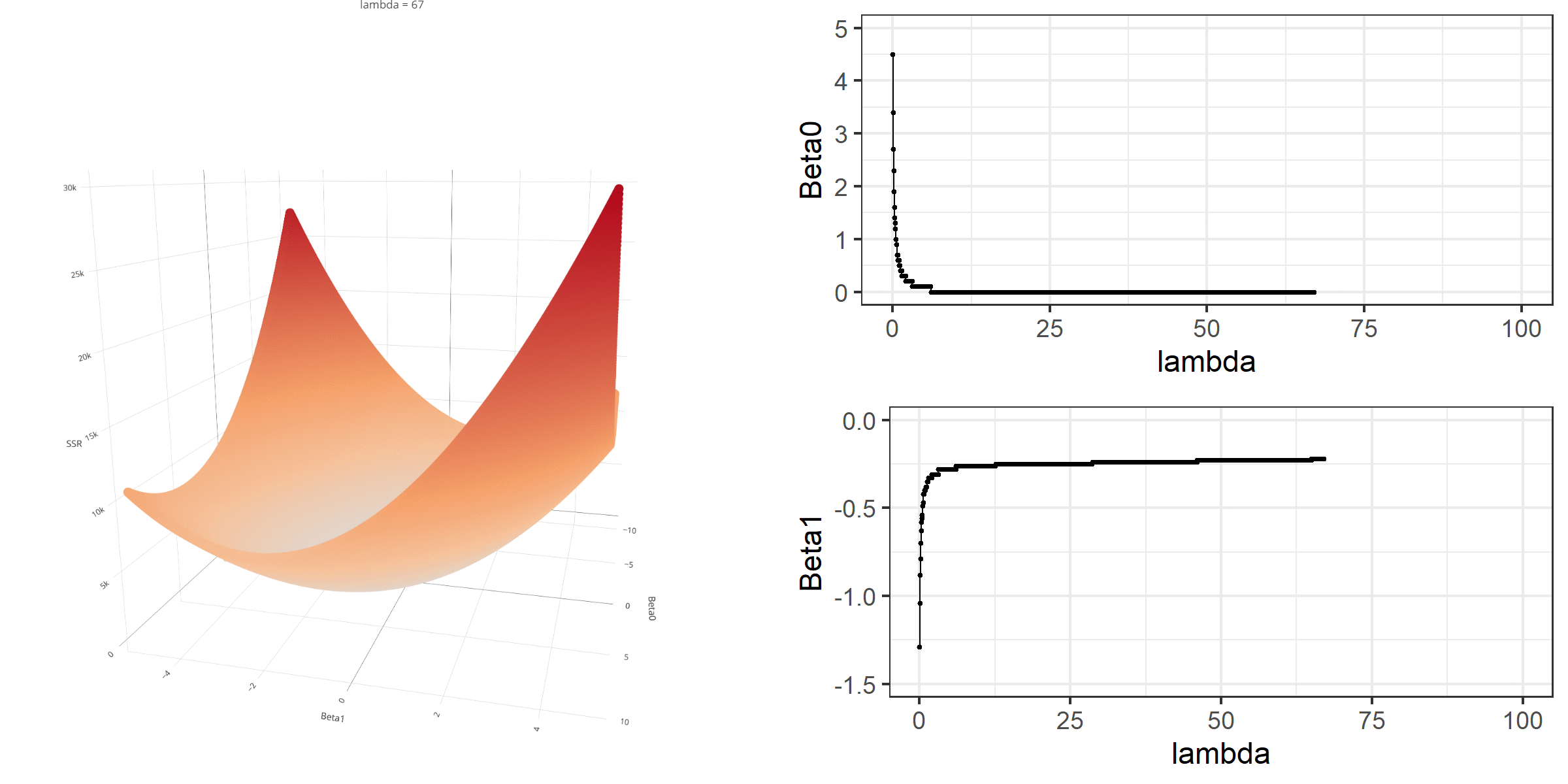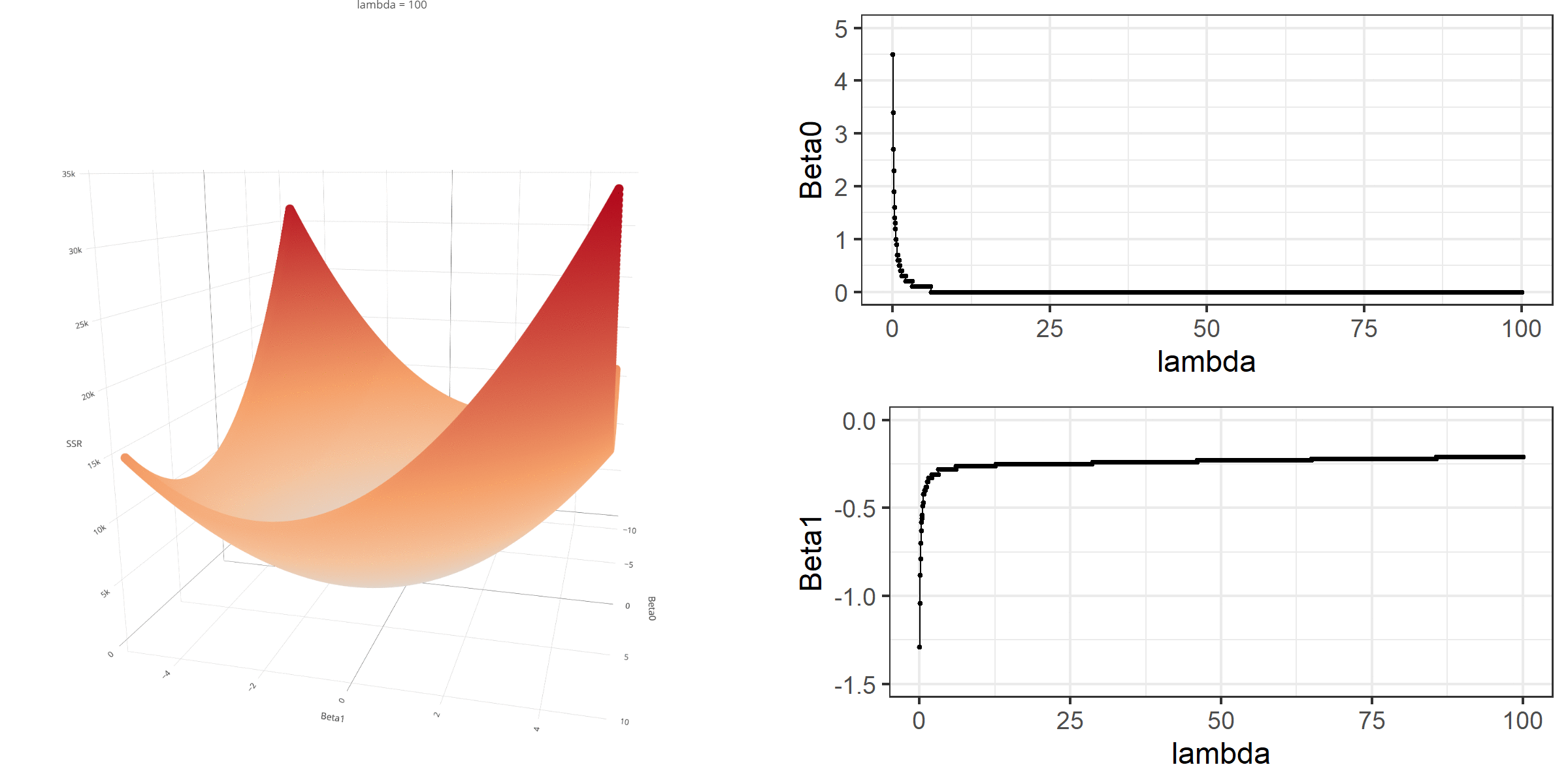
### Model Estimation

The matrix solution we learned before for regression without regularization can also be applied to estimate the coefficients from ridge regression given a specific `$\lambda$` value.

`$$\hat{\boldsymbol{\beta}} = (\mathbf{X^T}\mathbf{X} + \lambda \mathbf{I})^{-1}\mathbf{X^T}\mathbf{Y}$$`
  - `$\mathbf{Y}$` is an N x 1 column vector of observed values for the outcome variable, 
  - `$\mathbf{X}$` is an N x (P+1) **design matrix** for the set of predictor variables, including an intercept term,

- `$\boldsymbol{\beta}$` is an (P+1) x 1 column vector of regression coefficients,

- `$\mathbf{I}$` is a (P+1) x (P+1) identity matrix,

- and `$\lambda$` is a positive real-valued number,
  
---

Suppose we want to predict the readability score using the two predictors, Feature 220 ($X_1$) and Feature 166 ($X_2$). Our model will be

`$$Y_{(i)} = \beta_0  + \beta_1X_{1(i)} + \beta_2X_{2(i)} + \epsilon_{(i)}.$$`

If we estimate the ridge regression coefficients by using `$\lambda=.5$`, the estimates would be

{ `$\beta_0,\beta_1,\beta_2$` } = {-.915, 1.169, -0.221}.

.single[
.tiny[

```r
Y <- as.matrix(readability_sub$target)
X <- as.matrix(cbind(1,readability_sub$V220,readability_sub$V166))

lambda <- 0.5

beta <- solve(t(X)%*%X + lambda*diag(ncol(X)))%*%t(X)%*%Y

beta
```

```
           [,1]
[1,] -0.9151087
[2,]  1.1691920
[3,] -0.2206188
```
]]

---

If we change the value of λ to 2, we will get different estimates for the regression coefficients.

.single[
.tiny[

```r
Y <- as.matrix(readability_sub$target)
X <- as.matrix(cbind(1,readability_sub$V220,readability_sub$V166))

lambda <- 2

beta <- solve(t(X)%*%X + lambda*diag(ncol(X)))%*%t(X)%*%Y

beta
```

```
           [,1]
[1,] -0.7550986
[2,]  0.4685138
[3,] -0.1152953
```
]]

---

Suppose you manipulate the value of λ from 0 to 100 with increments of .1 and calculate the regression coefficients for different levels of `$\lambda$` values.

Note that the regression coefficients will shrink toward zero but will never be exactly equal to zero in ridge regression.

---

### Standardized variables

A critical complication arises in ridge regression when you have more than one predictor.

- Different scales of different variables will affect the magnitude of the unstandardized regression coefficients.
  
  - A regression coefficient of a predictor ranging from 0 to 100 will be very different from a regression coefficient of a predictor from 0 to 1. 
  
  - If we work with the unstandardized variables, the ridge penalty will be amplified for the coefficients of those variables with a more extensive range of values.

Therefore, it is critical that we standardize variables before we use ridge regression.

---

- When we standardize the variables, the mean of all variables becomes zero.

- Therefore, the intercept estimate for any regression model with standardized variables is guaranteed to be zero.

- The design matrix (**X**) doesn’t have to have a column of ones anymore because it is unnecessary (it would be a column of zeros if we had one).

.single[
.tiny2[

```r
Y <- as.matrix(readability_sub$target)
X <- as.matrix(cbind(readability_sub$V220,readability_sub$V166))
```
]]

.pull-left[
.single[
.tiny2[

```r
# Standardized Y

Y <- scale(Y)
 
Y
```

```
             [,1]
 [1,] -1.34512103
 [2,]  1.39315702
 [3,] -0.92104526
 [4,] -0.11446655
 [5,] -1.01147297
 [6,] -2.97759768
 [7,]  0.14541127
 [8,]  0.43376355
 [9,] -0.37229209
[10,] -0.24350754
[11,] -0.11722056
[12,]  0.75591253
[13,]  0.27743280
[14,]  0.91902756
[15,]  0.89029923
[16,]  1.18783003
[17,]  0.18827737
[18,]  0.43482354
[19,]  0.38586691
[20,]  0.09092186
attr(,"scaled:center")
[1] -0.7633224
attr(,"scaled:scale")
[1] 0.9660852
```
]]]

.pull-right[
.single[
.tiny2[

```r
# Standardized X

X <- scale(X)
 
X
```

```
             [,1]        [,2]
 [1,] -1.54285661  1.44758852
 [2,]  0.24727019 -0.47711825
 [3,] -0.55323997 -0.97867834
 [4,] -0.71812450  1.41817232
 [5,]  0.28072891 -0.62244962
 [6,] -1.23609737  0.11236158
 [7,]  1.33304531  0.34607530
 [8,] -2.06757849 -1.22697345
 [9,] -0.04732188  0.05882229
[10,] -0.11743882 -1.24554362
[11,]  0.87248435  1.93772977
[12,]  0.42065052  0.13025831
[13,] -0.66763117 -0.40479141
[14,]  0.98226625  1.39073712
[15,]  0.65999286  0.25182543
[16,]  0.15056337 -0.28808443
[17,] -0.45313072  0.02862469
[18,] -0.44667480  0.25187100
[19,]  2.01553800 -2.00805114
[20,]  0.88755458 -0.12237606
attr(,"scaled:center")
[1] 0.1683671 0.1005784
attr(,"scaled:scale")
[1] 0.19927304 0.06196686
```
]]]

---

The regression model's coefficients with standardized variables when there is no ridge penalty.

.single[
.tiny[

```r
lambda <- 0

beta.s <- solve(t(X)%*%X + lambda*diag(ncol(X)))%*%t(X)%*%Y

beta.s 
```

```
            [,1]
[1,]  0.42003881
[2,] -0.06335594
```
]]

The regression coefficients when the ridge penalty is increased to 0.5.

.single[
.tiny[

```r
lambda <- 0.5

beta.s <- solve(t(X)%*%X + lambda*diag(ncol(X)))%*%t(X)%*%Y

beta.s 
```

```
            [,1]
[1,]  0.40931629
[2,] -0.06215875
```
]]

---

Change in **standardized regression coefficients** when we manipulate the value of `$\lambda$` from 0 to 100 with increments of .1.

---

### Ridge regression with the `glmnet` package

Similar to the `lm()` function, we can use the `glmnet()` function from the `glmnet` package to run a regression model with ridge penalty.

There are many arguments for the glmnet() function. For now, the arguments we need to know are

- `x`: an N  x P input matrix, where N is the number of observations and P is the number of predictors

- `y`: an N x 1 input matrix for the outcome variable

- `alpha`: a mixing constant for lasso and ridge penalty. When it is 0, the ridge regression is conducted.

- `lambda`: penalty term

- `intercept`: set FALSE to avoid intercept for standardized variables

---

Regression with no penalty (traditional OLS regression)

- `alpha = 0` 
  
  - `lambda = 0`.

.single[
.tiny[

```r
require(glmnet)

Y <- as.matrix(readability_sub$target)
X <- as.matrix(cbind(readability_sub$V220,readability_sub$V166))
Y <- scale(Y)
X <- scale(X)

mod <- glmnet(x = X,
 y = Y,
 family = 'gaussian',
 alpha = 0,
 lambda = 0,
 intercept= FALSE)

coef(mod)
```

```
3 x 1 sparse Matrix of class "dgCMatrix"
                     s0
(Intercept)  .         
V1           0.42003881
V2          -0.06335594
```

]]

---

Increase the penalty term to 0.5.

- `alpha = 0` 
  
  - `lambda = 0.5`.

.single[
.tiny[

```r
require(glmnet)

Y <- as.matrix(readability_sub$target)
X <- as.matrix(cbind(readability_sub$V220,readability_sub$V166))
Y <- scale(Y)
X <- scale(X)

mod <- glmnet(x = X,
 y = Y,
 family = 'gaussian',
 alpha = 0,
 lambda = 0.5,
 intercept= FALSE)

coef(mod)
```

```
3 x 1 sparse Matrix of class "dgCMatrix"
                     s0
(Intercept)  .         
V1           0.27809880
V2          -0.04571182
```

]]

---

In Slide 14, when we estimate the ridge regression coefficients with `$\lambda=0.5$` using matrix solution, we got different numbers than whan the `glmnet()` function reports.

In the `glmnet()` function, it appears that the penalty term for the ridge regression is specified as

`$$\lambda N \sum_{i=1}^{P}\beta_p^2.$$`

For identical results, we should use `$\lambda = 0.5/20$` in the `glmnet()` package.

.single[
.tiny2[

```r
mod <- glmnet(x = X,
 y = Y,
 family = 'gaussian',
 alpha = 0,
 lambda = 0.5/20,
 intercept= FALSE)

coef(mod)
```

```
3 x 1 sparse Matrix of class "dgCMatrix"
                     s0
(Intercept)  .         
V1           0.40958102
V2          -0.06218857
```

]]

Note that these numbers are still slightly different.

The difference is due to the numerical approximation glmnet is using when optimizing the loss function. glmnet doesn’t use the closed-form matrix solution for ridge regression. This is a good thing because there is not always a closed form solution for different types of regularization approaches (e.g., lasso). Therefore, the computational approximation in glmnet is very needed moving forward.

---

### Tuning the Hyperparameter `$\lambda$`

In the context of machine learning, the parameters in a model can be classified into two types: parameters and hyperparameters.

- The **parameters** are typically estimated from data and not set by users. In the context of ridge regression, regression coefficients, {$\beta_0,\beta_1,...,\beta_P$}, are parameters to be estimated from data. 
  
  - The **hyperparameters** are not estimable because there are no first-order or second-order derivatives for these hyperparameters. Therefore, they must be set by the users. In the context of ridge regression, the penalty term, {$\lambda$}, is a hyperparameter.

The process of deciding what value to use for a hyperparameter is called **Tuning**.

It is usually a trial-error process. You try many different hyperparameter values and check how well the model performs based on specific criteria (e.g., MAE, MSE, RMSE) using k-fold cross-validation.

Then, you pick the value of a hyperparameter that provides the best predictive performance on cross-validation.

---

### Using Ridge Regression to Predict Readability Scores

Please review the following notebook for applying Ridge Regresison to predict readability scores from 768 features using the whole dataset.

[Predicting Readability Scores using the Ridge Regression](https://www.kaggle.com/code/uocoeeds/building-a-ridge-regression-model)

---

# Lasso Regression
---

### Lasso Penalty

Lasso regression is similar to the Ridge regression but applies a different penalty term.

$$ Penalty = \lambda \sum_{i=1}^{P} |\beta_p|,$$

- `$\lambda$` is the penalty constant,
  
  - `$|\beta_p|$` is the absolute value of the regression coefficient for the `$p^{th}$` parameter.

The loss function for the lasso regression to optimize:

`$$Loss = \sum_{i=1}^{N}\epsilon_{(i)}^2 + \lambda \sum_{i=1}^{P}|\beta_p|$$`

---

Let's consider the same example where we fit a simple linear regression model: the readability score is the outcome ($Y$) and Feature 229 is the predictor($X$).

`$$Y = \beta_0  + \beta_1X + \epsilon,$$`

Assume the set of coefficients are { `$\beta_0,\beta_1$` } = {-1.5,2}, so my model is

`$$Y = -1.5  + 2X + \epsilon.$$`
Then, the value of the loss function when `$\lambda=0.2$` would be equal to 18.467.

.pull-left[
.single[
.tiny2[

```r
d <- readability_sub[,c('V220','target')]

b0 = -1.5
b1 = 2

d$predicted <- b0 + b1*d$V220
d$error <- d$target - d$predicted

d
```

.pull-right[
.single[
.tiny2[

```r
lambda = 0.2

SSR <- sum((d$error)^2)
penalty <- lambda*(abs(b0) + abs(b1))
loss <- SSR + penalty

SSR
```

```
[1] 17.76657
```

```r
penalty
```

```
[1] 0.7
```

```r
loss
```

```
[1] 18.46657
```
]]]

---

Below is a demonstration of what happens to the loss function and the regression coefficients for increasing levels of loss penalty (λ) for Lasso regression.

![](lasso.gif)

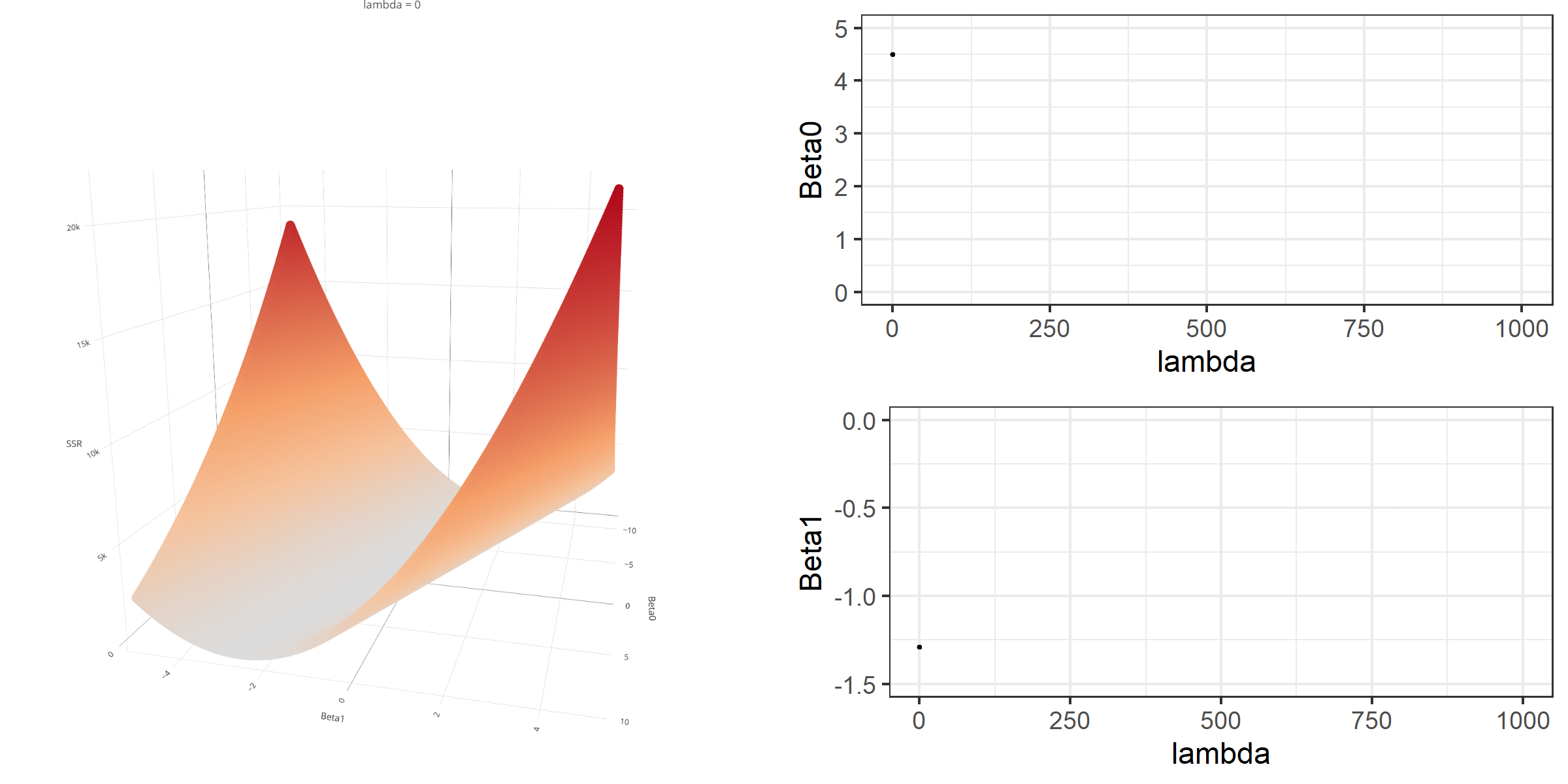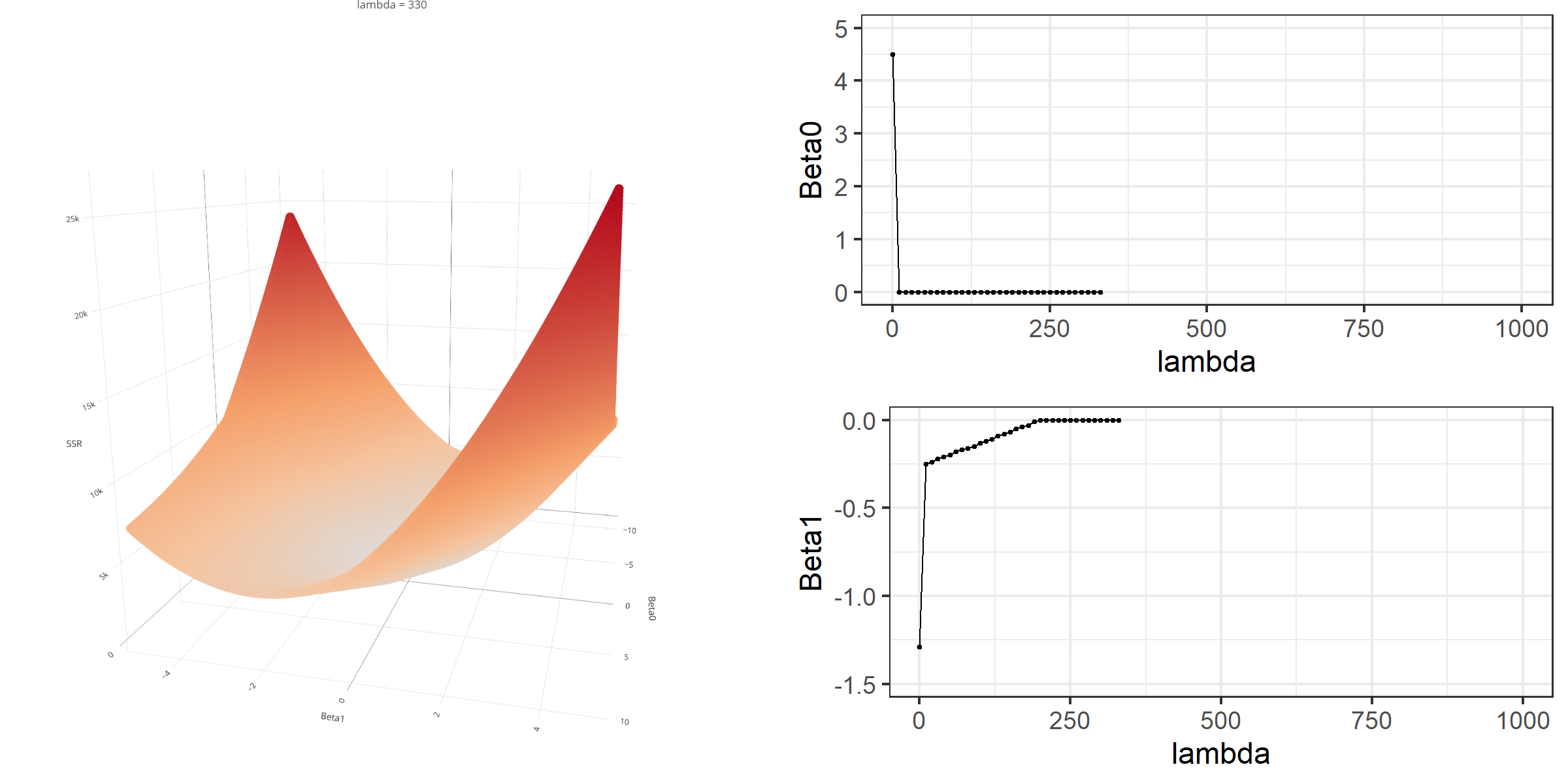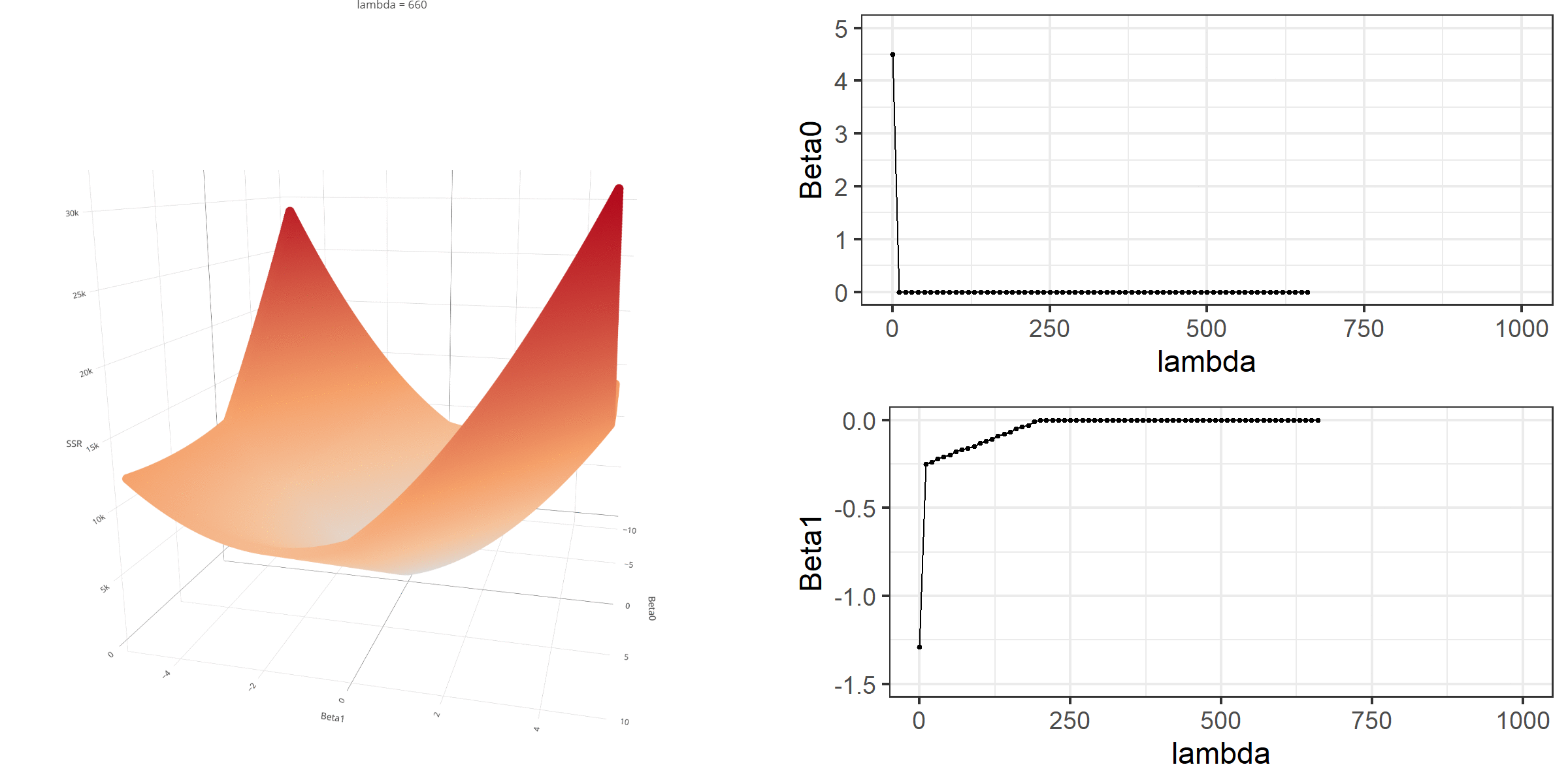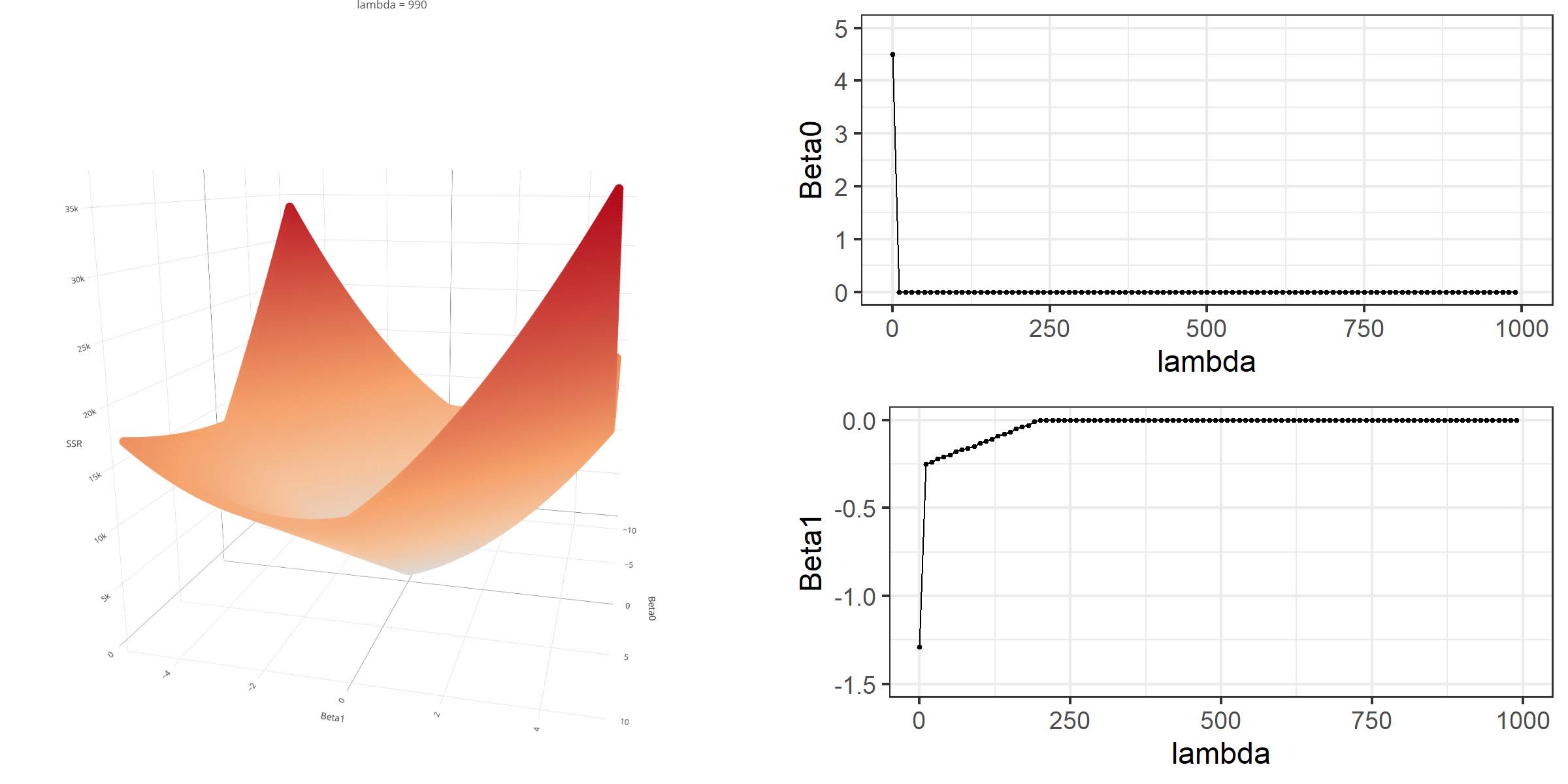
Note that the regression coefficients become equal to 0 at some point (this was not the case for ridge regression).

---

### Model Estimation via `glmnet()`

- There is no closed-form solution for lasso regression due to the absolute value terms in the loss function.

- The only way to estimate the coefficients of the lasso regression is to use numerical techniques and obtain computational approximations.

- Similar to ridge regression, glmnet is an engine we can use to estimate the coefficients of the lasso regression.

- The arguments are identical. The only difference is that we fix the `alpha=` argument to 1 for lasso regression.

.indent[
.single[
.tiny2[

```r
Y <- as.matrix(readability_sub$target)
X <- as.matrix(cbind(readability_sub$V220,readability_sub$V166))
Y <- scale(Y)
X <- scale(X)

mod <- glmnet(x = X,
 y = Y,
 family = 'gaussian',
 alpha = 1,
 lambda = 0.2,
 intercept=FALSE)

coef(mod)
```

```
3 x 1 sparse Matrix of class "dgCMatrix"
                   s0
(Intercept) .        
V1          0.2174345
V2          .        
```

]]]

---

- The `.` symbol for the coefficient of the second predictor indicates that it is equal to zero.

- While the regression coefficients in the **ridge regression** shrink to zero, they do not necessarily end up being exactly equal to zero.

- In contrast, **lasso regression** may yield a value of zero for some coefficients in the model.

- For this reason, lasso regression may be used as a variable selection algorithm. The variables with coefficients equal to zero may be discarded from future considerations as they are not crucial for predicting the outcome.

---

### Tuning `$\lambda$`

We implement a similar strategy for finding the optimal value of λ as we did for the Ridge Regression.

### Using Lasso Regression to Predict the Readability Scores

Please review the following notebook to apply Lasso Regression to predict readability scores from all 768 features using the whole dataset.

[Predicting Readability Scores using the Lasso Regression](https://www.kaggle.com/code/uocoeeds/building-a-lasso-regression-model)

---

# Elastic Net
---

Elastic net combines the two types of penalty into one by mixing them with some weighted average. The penalty term for the elastic net could be written as

`$$\lambda \left[ (1-\alpha)\sum_{i=1}^{P} \beta_p^2 + \alpha\sum_{i=1}^{P} |\beta_p|)\right].$$`

The loss function for the elastic net to optimize:

`$$Loss = \sum_{i=1}^{N}\epsilon_{(i)}^2 + \lambda \left[ (1-\alpha)\sum_{i=1}^{P} \beta_p^2 + \alpha\sum_{i=1}^{P} |\beta_p|)\right]$$`
- When `$\alpha$` is set to 1, this is equivalent to ridge regression.

- When `$\alpha$` equals 0, this is the equivalent of lasso regression.

- When `$\alpha$` takes any value between 0 and 1, this term becomes a weighted average of the ridge penalty and lasso penalty.

In Elastic Net, two hyperparameters will be tuned: `$\alpha$` and `$\lambda$`.

We can consider many possible combinations of these two hyperparameters and try to find the optimal combination using 10-fold cross-validation.

---

### Using Elastic Net to Predict the Readability Scores

Review of the following notebook for applying Elastic Net to predict readability scores from all 768 features using the whole dataset.

[Predicting Readability Scores using the Elastic Net](https://www.kaggle.com/code/uocoeeds/building-a-regression-model-with-elastic-net)

## Using the Prediction Model for a New Text

Review of the following notebook for predicting the readability of a given text with the existing model objects

[Predicting Readability Scores for a new text](https://www.kaggle.com/code/uocoeeds/using-the-prediction-models-for-a-new-text)